7. Aljabar Boolean, Penyederhanaan Logika dan Peta Karnaugh
Standard Forms of Boolean Expressions
- Sum of Product (SOP)
- Product of Sum (POS)
The Sum-of-Products (SOP) Form
When two or more product terms are summed by
Boolean
Conversion of a General Expression to SOP Form
Any logic expression can be change into SOP form by
applying Boolean Algebra techniques
The Standard SOP Form
The Products-of-Sum (POS) Form
When two or more sum terms are multiplied
The Standard POS Form
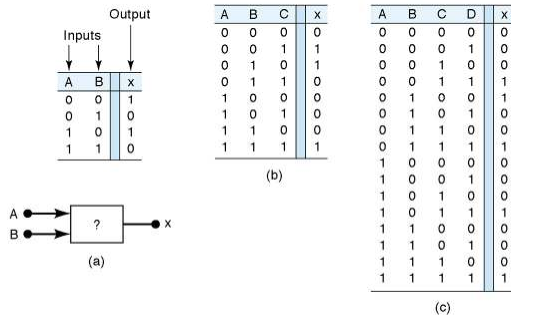
Boolean Expression and Truth Table
Converting SOP to Truth Table
- Examine each of the products to determine where the product is equal to a 1.
- Set the remaining row outputs to 0.
Converting POS to Truth Table
- Opposite process from the SOP expressions.
- Each sum term results in a 0.
- Set the remaining row outputs to 1.
Converting from Truth Table to SOP and POS
The Karnaugh Map
The Karnaugh Map
- Provides a systematic method for simplifying Boolean expressions
- Produces the simplest SOP or POS expression
- Similar to a truth table because it presents all of the possible values of input variables
The 3-Variable K-Map
The 4-Variable K-Map
K-Map SOP Minimization
- A 1 is placed on the K- Map for each product term in the expression.
- Each 1 is placed in a cell corresponding to the value of a product term
Example:
Map the following standard SOP expression on a K-Map:
Example:
Map the following standard SOP expression on a K-Map:
Exercise:
Map the following standard SOP expression on a K-Map:
Answer:
K-Map Simplification of SOP Expressions
- A group must contain either 1, 2, 4, 8 or 16 cells.
- Each cell in group must be adjacent to one or more cells in that same group but all cells in the group do not have to be adjacent to each other
- Always include the largest possible number 1s in a group in accordance with rule 1
- Each 1 on the map must be included in at least one group. The 1s already in a group can be included in another group as long as the overlapping groups include noncommon 1s To maximize the size of the groups and to minimize the number of groups
Example: Group the 1s in each K-Map
Determining the minimum SOP Expression from the Map
Groups the cells that have 1s. Each group of
cells containing 1s create one product term
composed of all variables that occur in only
one form (either uncomplemented or
complemented) within the group. Variable
that occurs both uncomplemented and
complemented within the group are
eliminated. These are called contradictory
variables.
Example:
Determine the product term for the K- Map below and write the resulting minimum SOP expression
Example: Use a K-Map to minimize the following standard SOP expression
Example: Use a K-Map to minimize the following standard SOP expression
Mapping Directly from a Truth Table
Don’t Care (X) Conditions
- A situation arises in which input variable combinations are not allowed
- Don’t care terms either a 1 or a 0 may be assigned to the output
Don’t Care (X) Conditions
Example of the use of “don’t
care” conditions to simplify an
expression
Exercise: Use K-Map to find the minimum SOP from
Comments
Post a Comment